C++线性时间的排序算法分析(2)
基数排序（Radix Sort）是一种非比较型排序算法，它将整数按位数切割成不同的数字，然后按每个位分别进行排序。基数排序的方式可以采用MSD（Most signi
基数排序（Radix Sort）是一种非比较型排序算法，它将整数按位数切割成不同的数字，然后按每个位分别进行排序。基数排序的方式可以采用MSD（Most significant digital）或LSD（Least significant digital），MSD是从最高有效位开始排序，而LSD是从最低有效位开始排序。
当然我们可以采用MSD方式排序，按最高有效位进行排序，将最高有效位相同的放到一堆，然后再按下一个有效位对每个堆中的数递归地排序，最后再将结果合并起来。但是，这样会产生很多中间堆。所以，通常基数排序采用的是LSD方式。
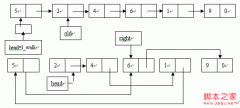
LSD基数排序实现的基本思路是将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。需要注意的是，对每一个数位进行排序的算法必须是稳定的，否则就会取消前一次排序的结果。通常我们使用计数排序或者桶排序作为基数排序的辅助算法。基数排序过程动画演示：Radix Sort
C++实现（使用计数排序）如下：
/*************************************************************************
> File Name: RadixSort.cpp
> Author: SongLee
************************************************************************/
#include<iostream>
using namespace std;
// 找出整数num第n位的数字
int findIt(int num, int n)
{
int power = 1;
for (int i = 0; i < n; i++)
{
power *= 10;
}
return (num % power) * 10 / power;
}
// 基数排序（使用计数排序作为辅助）
void RadixSort(int A[], int len, int k)
{
for(int i=1; i<=k; ++i)
{
int C[10] = {0}; // 计数数组
int B[len]; // 结果数组
for(int j=0; j<len; ++j)
{
int d = findIt(A[j], i);
C[d] += 1;
}
for(int j=1; j<10; ++j)
C[j] = C[j] + C[j-1];
for(int j=len-1; j>=0; --j)
{
int d = findIt(A[j], i);
C[d] -= 1;
B[C[d]] = A[j];
}
// 将B中排好序的拷贝到A中
for(int j=0; j<len; ++j)
A[j] = B[j];
}
}
// 输出数组
void print(int A[], int len)
{
for(int i=0; i<len; ++i)
cout << A[i] << " ";
cout << endl;
}
// 测试
int main()
{
int A[8] = {332, 653, 632, 5, 755, 433, 722, 48};
print(A, 8);
RadixSort(A, 8, 3);
print(A, 8);
return 0;
}
基数排序的时间复杂度是 O(k·n)，其中n是排序元素个数，k是数字位数。注意这不是说这个时间复杂度一定优于O(nlgn)，因为n可能具有比较大的系数k。
另外，基数排序不仅可以对整数排序，也可以对有多个关键字域的记录进行排序。例如，根据三个关键字年、月、日来对日期进行排序。
- 上一篇：C++实现第K顺序统计量的求解方法
- 下一篇：C++快速排序的分析与优化详解
精彩图集
精彩文章