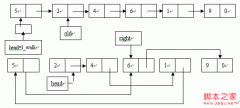
数据结构学习(C++)之单链表
节点类
#ifndef Node_H
#define Node_H
template
{
public:
Type data;
Node
Node() : data(Type()), link(NULL) {}
Node(const Type &item) : data(item), link(NULL) {}
Node(const Type &item, Node
};
#endif
【说明】因为数据结构里用到这个结构的地方太多了,假如用《数据结构》那种声明友元的做法,那声明不知道要比这个类的本身长多少。不如开放成员,事实上,这种结构只是C中的strUCt,除了为了方便初始化一下,不需要任何的方法,原书那是画蛇添足。下面可以看到,链表的public部分没有返回Node或者Node*的函数,所以,别的类不可能用这个开放的接口对链表中的节点操作。
【重要修改】原书的缺省构造函数是这样的Node() : data(NULL), link(NULL) {} 。我原来也是照着写的,结果当我做扩充时发现这样是不对的。当Type为结构而不是简单类型(int、……),不能简单赋NULL值。这样做使得定义的模板只能用于很少的简单类型。显然,这里应该调用Type的缺省构造函数。 这也要求,用在这里的类一定要有缺省构造函数。在下面可以看到构造链表时,使用了这个缺省构造函数。当然,这里是约定带表头节点的链表,不带头节点的情况请大家自己思考。
【闲话】请不要对int *p = new int(1);这种语法有什么怀疑,实际上int也可以看成一种class。
单链表类定义与实现
#ifndef List_H
#define List_H
#ifndef TURE
#define TURE 1
#endif
#ifndef FALSE
#define FALSE 0
#endif
typedef int BOOL;
#include "Node.h"
template
{
//基本上无参数的成员函数操作的都是当前节点,即current指的节点
//认为表中“第1个节点”是第0个节点,请注重,即表长为1时,最后一个节点是第0个节点
public:
List() { first = current = last = new Node
~List() { MakeEmpty(); delete first; }
void MakeEmpty() //置空表
{
Node
while (first->link != NULL)
{
q = first->link;
first->link = q->link;
delete q;
}
Initialize();
}
BOOL IsEmpty()
{
if (first->link == NULL)
{
Initialize();
return TURE;
}
else return FALSE;
}
int Length() const //计算带表头节点的单链表长度
{
Node
int count = 0;
while (p != NULL)
{
p = p->link;
count++;
}
return count;
}
Type *Get()//返回当前节点的数据域的地址
{
if (current != NULL) return ¤t->data;
else return NULL;
}
BOOL Put(Type const &value)//改变当前节点的data,使其为value
{
if (current != NULL)
{
current->data = value;
return TURE;
}
else return FALSE;
}
Type *GetNext()//返回当前节点的下一个节点的数据域的地址,不改变current
{
if (current->link != NULL) return ¤t->link->data;
else return NULL;
}
Type *Next()//移动current到下一个节点,返回节点数据域的地址
{
if (current != NULL && current->link != NULL)
{
prior = current;
current = current->link;
return ¤t->data;
}
else
{
return NULL;
}
}
void Insert(const Type &value)//在当前节点的后面插入节点,不改变current
{
Node
current->link = p;
}
BOOL InsertBefore(const Type &value)//在当前节点的前面插入一节点,不改变current,改变prior
{
Node
if (prior != NULL)
{
p->link = current;
prior->link = p;
prior = p;
return TURE;
}
else return FALSE;
}
BOOL Locate(int i)//移动current到第i个节点
{
if (i <= -1) return FALSE;
current = first->link;
for (int j = 0; current != NULL && j < i; j++, current = current->link)
prior = current;
if (current != NULL) return TURE;
else return FALSE;
}
void First()//移动current到表头
{
current = first;
prior = NULL;
}
void End()//移动current到表尾
{
if (last->link != NULL)
{
for ( ;current->link != NULL; current = current->link)
prior = current;
last = current;
}
current = last;
}
BOOL Find(const Type &value)//移动current到数据等于value的节点
{
if (IsEmpty()) return FALSE;
for (current = first->link, prior = first; current != NULL && current->data != value;
current = current->link)
prior = current;
if (current != NULL) return TURE;
else return FALSE;
}
BOOL Remove()//删除当前节点,current指向下一个节点,假如current在表尾,执行后current = NULL
{
if (current != NULL && prior != NULL)
{
Node
prior->link = p->link;
current = p->link;
delete p;
return TURE;
}
else return FALSE;
}
BOOL RemoveAfter()//删除当前节点的下一个节点,不改变current
{
if (current->link != NULL && current != NULL)
{
Node
current->link = p->link;
delete p;
return TURE;
}
else return FALSE;
}
friend ostream & operator << (ostream & strm, List
{
l.First();
while (l.current->link != NULL) strm << *l.Next() << " " ;
strm << endl;
l.First();
return strm;
}
protected:
/*主要是为了高效的入队算法所添加的。因为Insert(),Remove(),RemoveAfter()有可能改变last但没有改变last所以这个算法假如在public里除非不使用这些,否则不正确。但是last除了在队列中非常有用外,其他的时候很少用到,没有必要为了这个用途而降低Insert(),Remove()的效率所以把这部分放到protected,实际上主要是为了给队列继续*/ void LastInsert(const Type &value)
{
Node
last->link = p;
last = p;
}
void Initialize()//当表为空表时使指针复位
{
current = last = first;
prior = NULL;
}
//这部分函数返回类型为Node
Node
{
return current;
}
Node
{
prior = current;
current = current->link;
return current;
}
Node
{
return current->link;
}
Node
{
return first;
}
Node
{
return last;
}
Node
{
return prior;
}
void PutLast(Node
{
last = p;
}
//这部分插入删除函数不建立或删除节点,是原位操作的接口
void Insert(Node
{
p->link = current->link;
current->link = p;
}
void InsertBefore(Node
{
p->link = current;
prior->link = p;
prior = p;
}
void LastInsert(Node
{
p->link = NULL;
last->link = p;
last = p;
}
Node
{
if (current != NULL && prior != NULL)
{
Node
prior->link = current->link;
current = current->link;
return p;
}
else return NULL;
}
Node
{
if (current->link != NULL && current != NULL)
{
Node
current->link = current->link->link;
return p;
}
else return NULL;
}
private:
List(const List
Node
//尽量不要使用last,假如非要使用先用End()使指针last正确
};
#endif
【说明】我将原书的游标类Iterator的功能放在了链表类中,屏蔽掉了返回值为Node以及Node*类型的接口,这样的链表简单、实用,扩充性能也很好。
在完成书后作业的时候,我发现了原书做法的好处,也就是我的做法的不足。假如使用原书的定义,在完成一个功能时,只需要写出对应的函数实现。而在我的定义中,必须先派生一个类,然后把这个功能作为成员或者友元。但是这种比较并不说明书上的定义比我的要合理。首先,使用到原位操作的情况并不多,书后作业只是一种非凡情况;换句话说,书上的定义只是对完成书后作业更实用些。其次,在使用到链表的时候,通常只会用到插入、删除、取数据、搜索等很少的几个功能,我的定义足够用了。而在完成一个软件时,对链表的扩充功能在设计阶段就很清楚了,这时可以派生一个新类在整个软件中使用,对整体的规划更为有利。而对于单个链表的操作,把它作为成员函数更好理解一些。也就是说我的定义灵活性不差。
单链表应用
有人曾经建议最好把链表和链表位置这两个分开,C++标准库是这么做的;但对于初学者来说,一个类总比两个类好操作。我不清楚在书中这部分的程序究竟调没调试,但这种语句我是绝对看不懂的:
ListNode
ListIterator
ListIterator
pa = pc = Aiter.First(); pb = p = Biter.First();
………………………..
pa->coef = pa->coef + pb->coef;
p = pb; pb = Biter.Next(); delete p;
pa, pb, p 究竟指向什么?你说这很清楚,ListNode
假如从基本的节点操作入手,谁也不会弄的这么乱。但正因为又多了一个类,很多事就疏忽了。所以,我并不怀疑标准库的做法,只是对于初学者,同一时间最好只对一个类操作。我以我的定义为基础,重新完成了这段程序。我并不欣赏原位操作的多项式加法(+),PolyA+PolyB,然后B就嗖的一下没了,A就多了一堆(也可能少了一堆);你作intJ+intK的时候怎么没见J和K有什么变化。与其这样,重载“+”还不如写成PolyA.Add(PolyB)或者PolyAdd(PolyA,PolyB)。
一元多项式类定义与实现
#ifndef Polynomial_H
#define Polynomial_H
#include "List.h"
class Term
{
public:
int coef;
int eXP;
Term() : coef(0), exp(0) {}
Term(int c, int e) : coef(c), exp(e) {}
Term(int c) : coef(c), exp(0) {}
};
class Polynomial : List
{
public:
void Input()
{
cout << endl << "输入多项式的各项系数和指数";
cout << endl << "注重:请按降序输入各项,输入系数0表示结束" << endl;
int coef, exp;
for(int i = 1; ; i++)
{
cout << "第" << i << "项的系数:";
cin >> coef;
if (coef)
{
cout << "指数:";
cin >> exp;
Term term(coef, exp);
Insert(term);
}
else break;
}
}
void Print()
{
cout << endl;
First();
if (!IsEmpty())
{
Term *p = Next();
cout << p->coef;
if (p->exp)
{
cout << "x";
if (p->exp != 1) cout << "^" << p->exp;
}
while (Next() != NULL)
{
p = Get();
if (p->coef > 0) cout << "+";
cout << p->coef;
if (p->exp)
{
cout << "x";
if (p->exp != 1) cout << "^" << p->exp;
}
}
}
cout << endl;
}
friend void PolyAdd (Polynomial &polyA, Polynomial &polyB)
{
Node
polyA.First();polyB.First();
pA = polyA.pNext();pB = polyB.pNext();
while (pA != NULL && pB !=NULL)
{
if (pA->data.exp == pB->data.exp)
{
pA->data.coef = pA->data.coef + pB->data.coef;
polyB.Remove();
if (!pA->data.coef) polyA.Remove();
else polyA.pNext();
}
else
{
if (pA->data.exp > pB->data.exp)
{
polyB.pRemove();
polyA.InsertBefore(pB);
}
else if (pA->data.exp < pB->data.exp) polyA.pNext();
}
pA = polyA.pGet();pB = polyB.pGet();
}
if (pA == NULL)
{
polyA.pGetPrior()->link = pB;
polyB.pGetPrior()->link = NULL;
}
}
};
#endif
【说明】对于多项式,通常我们都是降序书写的,于是我就要求降序输入。但是对于做加法来说,确实升序的要方便一些,于是,实际上到了内部,就变成升序的了。对于输出格式(从C的时候我就不喜欢做这个),尽量照顾习惯,但是当非常数项系数为1的时候还是会输出系数的,我实在不想把一个实际应用中根本拿不出台的输出函数搞的很复杂。为我编起来方便,输出变成了升序的,请多包含。测试程序就不给了,很简单。在续篇中,我将完成一元多项式“+”“-”“×”“=”的重载――为什么没有“÷”,这种运算我拿笔算都不麻利,编起来就更闹心了,我还清楚的记得拿汇编写多字节除法程序时的痛苦。到了下一篇,你就可以这样写了a=b+c*d;a.Print()。
在下面将会有些重载运算符的例子,我们的工作将是使多项式的运算看起来更符合书写习惯。完成这些是我觉得我擅自将原书的“+”改成了PolyAdd(),总要给个交待吧。
下面将完成单链表的赋值运算的重载,请把这部分加到List类的public部分。的确,这部分也可以放在多项式类里实现;但是,复制一个多项式实际上就是复制一个单链表,与其单单做一个多项式赋值,还不如完成单链表的赋值,让派生类都能共享。
operator = (const List
{
MakeEmpty();
for (Node
}
还记得List类的private里面的这个List(const List
List(const List
{
first = current = last = new Node
for (Node
}
终于可以这样写了a = b + c * d
friend Polynomial operator + (Polynomial &polyA, Polynomial &polyB)
{
Polynomial tempA = polyA;Polynomial tempB = polyB;
PolyAdd(tempA, tempB);
return tempA;
}
friend Polynomial operator * (Polynomial &polyA, Polynomial &polyB)
{
Node
Node
Polynomial polyTempA, polyTempB;
int coef, exp;
if (pA == NULL pB == NULL) return polyTempA;
for (pA = polyA.pGetFirst()->link; pA != NULL; pA = pA->link)
{
for(pB = polyB.pGetFirst()->link; pB != NULL; pB = pB->link)
{
coef = pA->data.coef * pB->data.coef;
exp = pA->data.exp + pB->data.exp;
Term term(coef, exp);
polyTempB.LastInsert(term);
}
PolyAdd(polyTempA, polyTempB);
polyTempB.Initialize();
}
return polyTempA;
}
【后记】很显然,在“+”的处理上我偷懒了,但这是最方便的。乘法部分只要参照手工运算,还是很简单的,我就不解释了。对于“-”,可以先完成(-a)这样的算法,然后就可以用加法完成了,而你要是象我一样懒很可能就会做这种事-a=-1×a,真的不提倡,超低的效率。对于除法,假如你会用汇编写多字节除法(跟手工计算很像),依样画葫芦也能弄出来,但首先要完成“-”。假如要写又得好长,留给你完成吧。到这里你明白原位加法的重要了吧,这些运算实际上都是靠它实现的。
- 上一篇:用游戏串起程序员的基本功之二
- 下一篇:八皇后问题求解